OpenGL でテセレーションのシェーダー(TCS,TES)を使う

OpenGLの4.x世代でテセレーションのシェーダーが使えるようになり、DirectX11相当になりました。前回は簡単な三角形や四角形の再分割は作ってみたので、今回はモデル形状について適用してみたいと思います。
　そして割とテセレーションのサンプルでは定番の PN Triangles の方法で OpenGLのシェーダー Tessellation Control Shader(TCS), Tessellation Evaluation Shader(TES) を作成して描画してみたいと思います。

PN Trianglesについて

PN Triangles は、位置と法線の情報から曲面での再分割の位置を求めるためのアルゴリズムです。詳しくは論文の Curved PN Triangles を参考にしてください。
　DirectX での実装例はよく見かけるのですが、OpenGLでの実装についてはあまりやられているのを見かけませんでした。今回やってみて感じたのは特にOpenGLだから難しいということはない、ということです。それなのにサンプルが少ないのは残念ですね。

DirectX と OpenGL でのシェーダーの違い

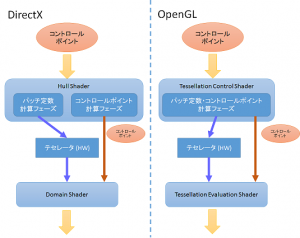
基本的には、ハルシェーダー=Tessellation Control Shader、 ドメインシェーダー=Tessellation Evaluation Shader と対応しています。しかし、ハルシェーダー部分が DirectX と OpenGL でちょっと違います。DirectX ではハルシェーダーと表現している部分の処理の中に、テセレーション係数を求めるためのパッチ係数フェーズとコントロールポイント出力フェーズの２つが含まれています（コントロールポイント出力フェーズでは後段へのデータ出力の役割もある模様）。
　OpenGLのTCSでは、パッチ係数フェーズとコントロールポイント出力フェーズを分けずに TCS内で一緒くたに記述してしまうのが作法のようです。一部の例では、パッチ係数を求めるときは下記のように gl_InvocationID で１回だけ実行されるようにしていたりするようです。

out TCS_OUT tcsOut[];
void main() {
  if( gl_InvocationID == 0 ) {
    /* パッチ係数算出のためのフェーズ */
    gl_TessLevelOuter[0] = 1;
    gl_TessLevelOuter[1] = 1;
    gl_TessLevelOuter[2] = 1;
    gl_TessLevelInner[0] = 1;
  }
  /* コントロールポイント処理 */
}

図示するとこんな感じでしょうか。

PN Trianglesを実装してみる

PN Trianglesを実装してみました。上記のDirectXでのシェーダーとGLでの対応関係がわかってしまえば、DirectXのサンプルを読み解いて、GLで実装し直すのもそこまで難しい話ではないように思います。
　また描画に関しては以前に説明したとおりの内容でモデル描画を行えばよいのでここでは実装したシェーダーを公開してみたいと思います(シェーダー内容は長めなコードになるので末尾を参照)。またプロジェクション変換は頂点が確定した後で行う必要があるので、今までは頂点シェーダーでやっていましたが、これからは TES(ドメインシェーダー) で行う必要があります。

描画結果

動画でキャプチャしてみました。

立方体をPN Trianglesしてみた。確かに割れてます

立方体だけど、８つの頂点の法線は隣接面の頂点と共有できるように合成したものを使用。このときちょっと丸みを帯びていきます。

モデルとして定番のteapot で PN Triangles を適用してみました。

シェーダー例

形状がわかりやすいように、カラー情報は法線を出力するようにしています。

layout( vertices = 3 ) out;

in VS_Out {
  vec3 WorldPos;
  vec3 Normal;
} fromVS[];

uniform float gTessellationLevel = 1;

struct TC_Output {
  vec3 Position;
  vec3 Normal;
};

out TC_Output TC_Out[];
void main() {
  if( gl_InvocationID == 0 ) {
   gl_TessLevelOuter[0] = gTessellationLevel;
   gl_TessLevelOuter[1] = gTessellationLevel;
   gl_TessLevelOuter[2] = gTessellationLevel;
   gl_TessLevelInner[0] = gTessellationLevel;
  }

  TC_Out[ gl_InvocationID ].Position = fromVS[ gl_InvocationID ].WorldPos;
  TC_Out[ gl_InvocationID ].Normal = fromVS[ gl_InvocationID ].Normal;
}

layout( triangles, equal_spacing, ccw ) in;

uniform mat4 gVP;


struct TC_Output {
  vec3 Position;
  vec3 Normal;
};
in TC_Output inPatch[];

out vec4 vsout_col;

void main() {

  vec3 p1 = inPatch[0].Position;
  vec3 p2 = inPatch[1].Position;
  vec3 p3 = inPatch[2].Position;

  vec3 b300 = p1;
  vec3 b030 = p2;
  vec3 b003 = p3;

  vec3 n1 = inPatch[0].Normal;
  vec3 n2 = inPatch[1].Normal;
  vec3 n3 = inPatch[2].Normal;
  vec3 n200 = n1;
  vec3 n020 = n2;
  vec3 n002 = n3;

  float w12 = dot( (p2-p1), n1 );
  vec3 b210 = (2.0 * p1 + p2 - w12 * n1) / 3.0;

  float w21 = dot( (p1 - p2), n2 );
  vec3 b120 = (2.0 * p2 + p1 - w21 * n2) / 3.0;

  float w23 = dot( ( p3 - p2 ), n2 );
  vec3 b021 = (2.0 * p2 + p3 - w23 * n2 ) / 3.0;
    
  float w32 = dot( ( p2 - p3 ), n3 );
  vec3 b012 = ( 2.0 * p3 + p2 - w32 * n3 ) / 3.0;

  float w31 = dot( ( p1 - p3 ), n3 );
  vec3 b102 = ( 2.0 * p3 + p1 - w31 * n3 ) / 3.0;
    
  float w13   = dot( ( p3 - p1 ), n1 );
  vec3 b201 = ( 2.0 * p1 + p3 - w13 * n1 ) / 3.0;
    
  vec3 e    = ( b210 + b120 + b021 + b012 + b102 + b201 ) / 6.0;
  vec3 vPos = ( p1 + p2 + p3 ) / 3.0;
  vec3 b111 = e + ( ( e - vPos ) / 2.0 );

  float v12 = 2.0 * dot( ( p2 - p1 ), ( n1 + n2 ) ) / dot( ( p2 - p1 ), ( p2 - p1 ) );
  vec3 n110  = normalize( ( n1 + n2 - v12 * ( p2 - p1 ) ) );

  float v23  = 2.0 * dot( ( p3 - p2 ), ( n2 + n3 ) ) / dot( ( p3 - p2 ), ( p3 - p2 ) );
  vec3 n011  = normalize( ( n2 + n3 - v23 * ( p3 - p2 ) ) );

  float v31  = 2.0 * dot( ( p1 - p3 ), ( n3 + n1 ) ) / dot( ( p1 - p3 ), ( p1 - p3 ) );
  vec3 n101  = normalize( ( n3 + n1 - v31 * ( p1 - p3 ) ) );

  //----
  float u = gl_TessCoord.x;
  float v = gl_TessCoord.y;
  float w = gl_TessCoord.z;
  float uu = u * u, vv = v * v, ww = w * w;
  float uu3 = 3.0 * uu, vv3 = 3.0 * vv, ww3 = 3.0 * ww;

  vec3 interpPosition = 
	p1 * w * ww + 
	p2 * u * uu + 
	p3 * v * vv +
	b210 * ww3 * u +
	b120 * uu3 * w +
	b201 * ww3 * v +
	b021 * uu3 * v +
	b102 * vv3 * w +
	b012 * vv3 * u +
	b111 * 6.0 * w * u * v;

  gl_Position = gVP * vec4( interpPosition, 1.0 );

  vec3 interpNormal = inPatch[0].Normal * ww + inPatch[1].Normal * uu + inPatch[2].Normal * vv 
    + n110 * w * u 
	+ n011 * u * v
	+ n101 * w * v;
  vec3 normal = normalize( interpNormal );

  vsout_col.w = 1;
  vsout_col.xyz = normal * 0.5;
  vsout_col.xyz += 0.5;
}