ディフューズマテリアル
シンプルなディフューズマテリアル
光を放出しないオブジェクトは、単に周囲の色を受け、固有の色でそれを変調します。表面で反射した光はランダムな方向になります。たとえば2つのディフューズマテリアルの間に光を送り込むと、反射した光は全く別の方向に向くことになります。
ある曲面のヒットポイント p に接する単位半径の球体がある。ヒットポイント上での法線を n とし、この2つの球体の中心は (p+n), (p-n) となる。曲面の外側である (p+n) の球の内側にあるランダムな点 S を選び、ヒットポイントから点Sにレイを飛ばします。
子レイの数を制限する
ray_color 関数は再帰関数です。この再帰がいつ終了するか、という点を気にする必要があります。場合によってはかなり多くの再帰処理によってスタックオーバーフローを引き起こします。これを防ぐために再帰数を制限し、それに到達したときには光の寄与を返さないようにします。
これらの処理を実装して画像をレンダリングさせると以下の結果が得られます。

正確な色強度のためのガンマ補正の使用
この球の下の影に着目します。暗い画像になっていますが、球体は各反射で半分のエネルギーしか吸収しないので 50% の反射板になっています。多くの画像ビューワーは画像が「ガンマ補正」されていると仮定しているために暗く見えます。ここでは最初の近似としてガンマ2を使います。
これらの処理を色データを書き出す直前に行います。 pow(c,1.0 /2.0 ) で変換しますが、これは平方根を計算するのと同じです。
void write_color(std::ostream& out, color pixel_color, int samples_per_pixel) {
auto r = pixel_color.x();
auto g = pixel_color.y();
auto b = pixel_color.z();
// Divide the color total by the number of samples and gamma-correct for gamma=2.0.
auto scale = 1.0 / samples_per_pixel;
r = sqrt(r * scale);
g = sqrt(g * scale);
b = sqrt(b * scale);
// Write the translated [0,255] value of each color component.
out << static_cast<int>(256 * clamp(r, 0.0, 0.999)) << ' '
<< static_cast<int>(256 * clamp(g, 0.0, 0.999)) << ' '
<< static_cast<int>(256 * clamp(b, 0.0, 0.999)) << '\n';
}これらの処理を行い出力した画像は以下の通りです。

アクネの修正
ここで奇妙なバグがあります。反射されたレイのいくつかは t=0 ではなく t=0.0000001 や t=0.00000001 などの浮動小数点近似値で反射している物体に当たってしまいます。よってゼロに近い部分は無視する必要があります。
真のランバート反射
表面法線に沿ってオフセットされた単位球内のランダムな点を生成する方法は、 法線に近い部分で半球状の方向を高い確率で選択し、すれすれの角度でレイを散乱する確率が低いことに対応しています。この分布は、入射角 φ (法線からの角度)が (cosφ)^3 によってスケーリングされます。
しかし我々は cosφの分布を持つランバーティアンに興味があります。 真のランバーティアン分布は、法線に近いレイ散乱のほうが確率が高くなるが、分布はより均一になります。これは表面法線にそってオフセットされた単位球の表面上の点を選ぶことによって実現できます。この表面上の点を選ぶことは、単位球内の点を選んだ後、正規化することで求められます。
金属
マテリアルの抽象クラス
異なるオブジェクトに異なるマテリアルを使いたいので、マテリアルの抽象クラスを導入します。抽象クラスにより動作をカプセル化します。マテリアルクラスには散乱のレイを生成、レイの減衰を計算するメソッドを用意します。
光の散乱と反射のモデリング
すでにあるランバート計算を、このマテリアルクラスを継承して実装します。
ミラーリングされた光の反射
滑らかな金属の場合、光はランダムに散乱しません。ここでは v + 2b で反射ベクトルを計算します。
シーンに2つの金属球を追加してレンダリングした結果が以下です。

ファジーリフレクション
小さな球を用いて、光の新しい端点を選択することにより反射法校をランダム化することも出来ます。球が大きいほど反射はぼやけます。
ファジーパラメータをメタルマテリアルに導入し、scatter メソッドを修正します。
class metal : public material {
public:
metal(const color& a, double f) : albedo(a), fuzz(f < 1 ? f : 1) {}
virtual bool scatter(
const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
) const {
vec3 reflected = reflect(unit_vector(r_in.direction()), rec.normal);
scattered = ray(rec.p, reflected+fuzz*random_in_unit_sphere());
attenuation = albedo;
return (dot(scattered.direction(), rec.normal) > 0);
}
public:
color albedo;
double fuzz;
};
誘電体
水やガラス、ダイヤモンドなどの透明な物質は誘電体です。光がこれらに当たると反射と屈折(透過)に分かれます。
屈折
屈折光はデバッグが最も難しいです。
スネルの法則
屈折はスネルの法則で説明されます。この式は法線からの角度 θ、θ’ 、そして屈折率 η、η’ で表現されています。空気の屈折率=1.0, ガラス=1.3~1.7, ダイヤモンド=2.4 です。
屈折した光の方向を決めるために、 sin θ’ について解く必要があります。
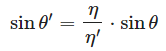
表面で屈折した側には屈折したレイR’と法線n’ があり、これらの角度はθ’ です。ここで R’ を次のように分割します。
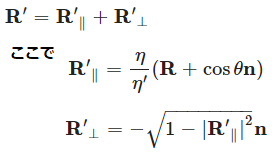
ここで cosθ を解く必要がありますが、内積を用いて式を変形します。
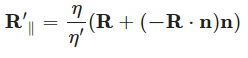
これらの結果より関数を実装します。
vec3 refract(const vec3& uv, const vec3& n, double etai_over_etat) {
auto cos_theta = dot(-uv, n);
vec3 r_out_parallel = etai_over_etat * (uv + cos_theta*n);
vec3 r_out_perp = -sqrt(1.0 - r_out_parallel.length_squared()) * n;
return r_out_parallel + r_out_perp;
}右側の球体に屈折率 1.3 のマテリアルを適用して描画したものが以下です。屈折率 1.0 (空気)にすると当然ですが、見えないオブジェクトになります。

全反射
確かにおかしいです。現実的なやっかいな問題として、光が屈折率の高い物体の中にあるとき、スネルの法則の実数解がないので屈折が出来ないと言うことがあります。スネルの法則と sinθ’ の式を見ると以下の通りでした。
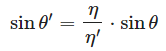
レイがガラス中から空気中へ出る場合では、 η=1.5, η’=1.0 の場合となります。
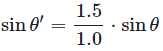
sinθ’ は 1.0 以上になりえないので、この等式は成立できません。このとき屈折は発生せず、光を全反射しなければなりません。

シュリック近似
実際のガラスの反射率は角度によって変化します。急な角度で窓を見ると、鏡になります。これには大きな醜い方程式がありますが、多くの人が Christophe Schlickによる安価で驚くほど正確な多項式近似を使用しています。
中空ガラス玉のトリックについて
球の内部にさらにオブジェクトを配置して、そのときに半径をマイナスに設定すると中空ガラス玉の見た目ができるらしいです。手元で同じようにやってみたところ以下の画像を得ました。映り込みもありますし、それっぽいですね。

位置決め可能なカメラ
視野角と位置を決めてレンダリングするため、カメラの実装を変更します。
いわゆるカメラのビュー行列の話になるためここでは割愛します。

デフォーカスぼかし
デフォーカスぼかし、被写界深度と呼ぶものについてです。
薄いレンズ
実際のカメラには複雑な複合レンズがありますが、グラフィックスの人々は通常薄いレンズ近似を使用します。
サンプリングのレイを生成する
通常すべてのシーンのレイは lookfrom ポイントから生成します。デフォーカスぼかしを行うには、 lookfrom ポイントを中心としたディスクの内側からランダムなレイを生成します。今までの元のカメラは半径 0 のデフォーカスディスクを持っている(=ぼけない)と考えることが出来ます。
これらの実装をカメラクラスに行って、以下の画像を得ることが出来ました。確かにボケがでています。

ちょっとボケが強かったので、パラメータを変更(aperture = 0.5)してレンダリングさせてみました。

最終章
Ray Tracing in One Weekend の最終章では、たくさんの球体を配置して表紙にもなっている画像を生成させます。

感想
レイトレーシングの勉強のために RayTracing in One Weekend をやってみました。各ステップで実行結果が見えて、また少しずつ拡張していくやり方のため、楽しみながら進められることが出来たと思います。ラスタライズ方式と違ってレイを飛ばしたときに、同処理をして色を決定するのか、という箇所は勉強になりました。基本的な構造はラスタライズ方式に比べてシンプルで、再帰処理を用いると本当にコードは少なく実装できるものだと感心しました。
レイトレーシングへの入門としてはとてもよかったです。ここからよりリアルな方向への拡張、処理速度向上へのトライなどがあるので、よい教材でした。
