ここ最近、DXR (DirectX RayTracing) を触っていましたが、原点に返って勉強してみることにしました。そこで Ray Tracing In One Weekend の内容をやってみることにしました。本家の内容を自分なりの意訳しつつやってみて、その内容をここに記載します。記載のコードは本家のものとは少し違っている部分がありますが、多くの部分で本家と同様です。そのため自分が変えてみた部分だけを記載します。
※ Ray Tracing In One Weekend の著作権は、 Peter Shirley さんにあります。
作るもの・はじめに
専用の API を使わずに C++ でレイトレーシングのプログラムをフルスクラッチで作成します。フル機能のレイトレーサーではないが、映画で使われるレイトレーシングの定番「間接照明」を備えます。もっとよりよいレイトレーサーに拡張するとき、このプログラムをベースに拡張していくのがよいでしょう。
ここで注意点です。”レイトレーシング”と誰かが言ったとき、それは多くのことを意味している可能性があります。ここで説明しようとしているのは、技術的にはパストレーサーです。コードはシンプルなものですが、出力される画像には満足するものと思います。
画像を出力する
レンダラーを作るときには、画像を表示する方法が必要です。最も簡単な方法はファイルに書き込むことですが、多種多様なフォーマットが存在します。一般的な画像フォーマットは複雑なので、プレーンテキストで構成される ppm フォーマットで始めます。また、長時間のレンダリングの進行状況を示すための進行状況インジケーターを追加しておきます。
しかし標準出力に書き込まれるよりはファイルに書き出したいため、 std::cout ではなく ofstream を用意してそちらに書き込むようにしました。
#include <iostream>
#include <fstream>
int main() {
const int image_width = 256;
const int image_height = 256;
std::ofstream file("result.ppm");
file << "P3\n" << image_width << ' ' << image_height << "\n255\n";
for (int j = image_height - 1; j >= 0; --j) {
std::cerr << "\rScanlines remaing: " << j << ' ' << std::flush;
for (int i = 0; i < image_width; ++i) {
auto r = double(i) / (image_width - 1);
auto g = double(j) / (image_height - 1);
auto b = 0.25;
int ir = static_cast<int>(255.999 * r);
int ig = static_cast<int>(255.999 * g);
int ib = static_cast<int>(255.999 * b);
file << ir << ' ' << ig << ' ' << ib << '\n';
}
}
std::cerr << "\nDone.\n";
return 0;
}Vec3 クラス
幾何学的ベクトルと色を格納するためのクラスとして Vec3 クラスを用意します。色、位置、方向、オフセットなどで使用します。色と位置で型が同じため代入できてしまいますが、コードを短くするためこのままです。エイリアスを定義しておいて、少しだけ見分けが付くようにしておきます。
ray.h ファイルを作成し、Ray クラスとベクトルのユーティリティ関数を用意しておきます。次に、色を書き込むための関数を用意します。color.h ファイルを作成し、引数で指定された色をストリームに書き込みます。
以上、用意したものを使って出力するようにメイン関数を修正します。
#include "color.h"
#include "vec3.h"
#include <iostream>
#include <fstream>
int main() {
const int image_width = 256;
const int image_height = 256;
std::ofstream file("result.ppm");
file << "P3\n" << image_width << ' ' << image_height << "\n255\n";
for (int j = image_height - 1; j >= 0; --j) {
std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
for (int i = 0; i < image_width; ++i) {
color pixel_color(double(i) / (image_width - 1), double(j) / (image_height - 1), 0.25);
write_color(file, pixel_color);
}
}
std::cerr << "\nDone.\n";
return 0;
}シンプルなカメラ、レイ、背景
すべてのレイトレーサーで共通なことは、レイのクラスと、レイに沿って表示される色の計算です。ここでレイを関数 P(t) = A + tB と考えます。Aはレイの原点、B は レイの方向です。パラメータ t によって直線上で点が決まります。正の t の場合、Aよりも前にあたる部分だけを得ることができ、これは半直線やレイと呼ばれているものになります。
ここでこのレイを表現するためのクラスとして ray.h ファイルを用意します。
シーンにレイを飛ばす
レイトレーシングでメインとなる処理は以下の通りです。
- 視点からピクセルへのレイを計算
- レイが交差するオブジェクトの決定
- 交差点の色を計算
正方形の画像を用いるとデバッグに苦労したようで、正方形ではない 16:9 画像を使用するようにします。
レイが通過する仮想的なビューポートを設定します。標準的な正方形ピクセルでは、ビューポートのアスペクト比はレンダリングされた画像と同じにします。ビューポートの高さを2単位にして、投影平面と投影点の距離は1単位にします。これは”focal length”と呼び、後に出てくる “focus distance” と混同しないようにしましょう。特に日本語だとどちらも「焦点距離」と訳されるようなので注意が必要そうでした。
カメラの中心である視点の位置を (0,0,0) とします。右手系の座標を用いて、Y-up, 右方向を +X とします。画面上の点を示すための (u, v) によってレイの終点が決まります。これを移動して画面の左下からトラバースします。(実際にはレイは方向であるので、画面上の点が終点となるわけではない。ベクトルを求めているだけに過ぎない)
ここでレイの方向ベクトルを正規化しないように、と記載がありました。
ray_color 関数では、レイの方向を正規化してYの高さに応じて白と青を線形補間で色を決定しています。以上、ここまでの内容を実行すると、以下に示す画像が得られます。
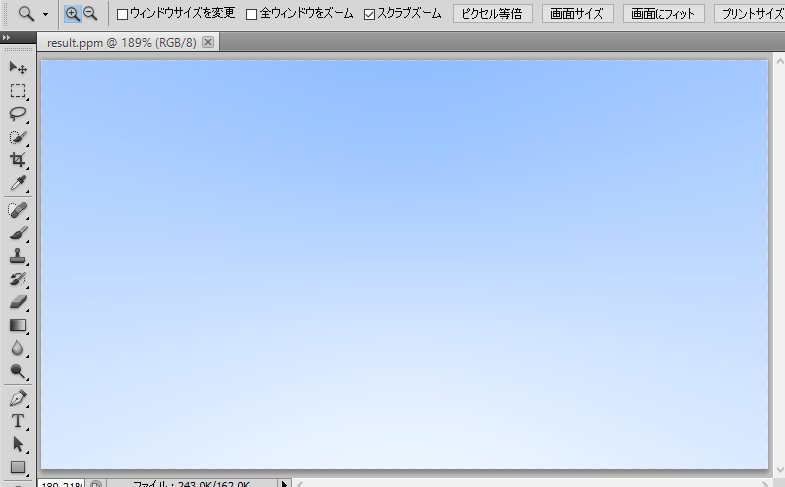
スフィアの追加
レイと球(スフィア)の判定は、言い換えると直線と円が交差するかの判定になります。 これらの関係式を求めて、交点を求めるようにして式変形を行います。
すると直線のパラメータtに対しての2次方程式の形に出来ます。ここで2次方程式の解の公式より、実数解が存在するかどうかの判別式を用いて、交点が存在するかどうか、という判定を行います。この処理を hit_sphere 関数で行います。
bool hit_sphere(const point3& center, double radius, const ray& r) {
vec3 oc = r.origin() - center;
auto a = dot(r.direction(), r.direction());
auto b = 2.0 * dot(oc, r.direction());
auto c = dot(oc, oc) - radius * radius;
auto discriminant = b * b - 4 * a * c;
return (discriminant > 0);
}この処理結果によって以下の画像が出力されます。

サーフェース法線と複数のオブジェクト
シェーディングするためにサーフェース法線を取得します。これは交点でサーフェースに垂直なベクトルです。コード上で強制するものではありませんが、法線を単位長に正規化しておくことでシェーディング時に便利なことがあります。球体の場合、外向きの法線は交点の場所から中心を引いた方向になります。
法線を確認するために1つのテクニックを使います。法線が正規化されている場合、各成分は -1から1 の範囲にあります。一方カラーは 0 から 1の範囲になります。係数とオフセットにより N(x,y,z)を C(r,g,b) へとマッピングします。法線を計算するには、交差した点 n を求めることが必要です。
このような処理をするように hit_sphere() 関数を修正します。
double hit_sphere(const point3& center, double radius, const ray& r) {
vec3 oc = r.origin() - center;
auto a = dot(r.direction(), r.direction());
auto b = 2.0 * dot(oc, r.direction());
auto c = dot(oc, oc) - radius * radius;
auto discriminant = b * b - 4 * a * c;
if (discriminant < 0)
{
return -1.0;
}
else
{
return (-b - sqrt(discriminant)) / (2.0 * a);
}
}以上の内容を実行すると、法線を可視化した結果を得ることができます。

交差コードの簡略化
ベクトルを自身と内積をとるとベクトルの長さの二乗になります。そして、解の公式での係数 b に着目し、 b=2h とおいて式を簡略化します。
結果、 (-h ± sqrt(h*h – a*c))/a という式を導出できます。
交差可能なオブジェクトの抽象化
複数の球について考えてみましょう。球の配列を作成するのは簡単ですが、レイが衝突するかもしれない何かという抽象クラスを作成し、球体と球体のリストの両方を作るだけで対応できるようにします。
クラスの名前付けに困るところではありますが、 Hittable でいくことにします。 (オブジェクトと呼ぶには一般的すぎますし、Surface もまたよく使用される名前なので避けておきます)。
hittable クラスは、レイを引数にとる関数を持っています。多くのレイトレーサーは tmin から tmax までの有効な範囲を設定して、 t がこの範囲に入っているときにのみヒットと判定するようにすると便利です。設計上の課題の1つに、何かにぶつかったときに法線を計算するようなことをするかどうか、という点があります。探索をしているうちに、より近いものに当たってしまうかもしれず、一番近くでヒットしたものの法線のみが必要になります。
struct hit_record {
point3 p;
vec3 normal;
double t;
};
class hittable {
public:
virtual bool hit(const ray& r, double t_min, double t_max, hit_record& rec) const = 0;
};これを用いて球のコードを作成します。 今までは hit_sphere 関数や ray_color 関数で処理していたものがキレイに整理されつつあります。
#include "hittable.h"
#include "vec3.h"
class sphere: public hittable {
public:
sphere() {}
sphere(point3 cen, double r) : center(cen), radius(r) {};
virtual bool hit(const ray& r, double tmin, double tmax, hit_record& rec) const;
public:
point3 center;
double radius;
};
bool sphere::hit(const ray& r, double t_min, double t_max, hit_record& rec) const {
vec3 oc = r.origin() - center;
auto a = r.direction().length_squared();
auto half_b = dot(oc, r.direction());
auto c = oc.length_squared() - radius*radius;
auto discriminant = half_b*half_b - a*c;
if (discriminant > 0) {
auto root = sqrt(discriminant);
auto temp = (-half_b - root)/a;
if (temp < t_max && temp > t_min) {
rec.t = temp;
rec.p = r.at(rec.t);
rec.normal = (rec.p - center) / radius;
return true;
}
temp = (-half_b + root) / a;
if (temp < t_max && temp > t_min) {
rec.t = temp;
rec.p = r.at(rec.t);
rec.normal = (rec.p - center) / radius;
return true;
}
}
return false;
}前面と背面
法線について2つめの設計上の取り決めとして、法線が常に指摘するかどうかです。現在見つかった法線は常に中心から交点への方向となり、法線は球体の外側を指しています。レイが内部から球に交差する場合、法線を内側に向ける、ということもできます。今までの実装では内側から衝突しても外側を向いています。
こういったものが必要かどうかについて、最終的にはレイがサーフェースのどちら側から来るのか、を判断するためです。表面裏面でそれぞれ異なるようにレンダリングされるオブジェクトや、ガラス玉のように内側と外側があるオブジェクトの場合に重要になります。
Hittable オブジェクトのリスト
レイと交差する汎用オブジェクトのリストクラスを作成し、 hittable_list.h を用意します。
一般定数とユーリティティ関数
rtweekend.h ファイルとして、以下の内容で用意します。後ほど無限大や円周率(π)が必要になります。
#ifndef RTWEEKEND_H
#define RTWEEKEND_H
#include <cmath>
#include <cstdlib>
#include <limits>
#include <memory>
// Usings
using std::shared_ptr;
using std::make_shared;
using std::sqrt;
// Constants
const double infinity = std::numeric_limits<double>::infinity();
const double pi = 3.1415926535897932385;
// Utility Functions
inline double degrees_to_radians(double degrees) {
return degrees * pi / 180;
}
// Common Headers
#include "ray.h"
#include "vec3.h"
#endif 今までに作成したものを用いて、 main を書き直します。
衝突の判定が hittable_list にお任せするようになり、シンプルになります。
また、球体を2つここで追加します。1つは今までに表示されていたものですが、もう1つは巨大な球として、床に相当するものを配置しています。地球みたいなものですね。
#include "rtweekend.h"
#include "hittable_list.h"
#include "sphere.h"
#include "color.h"
#include <iostream>
#include <fstream>
color ray_color(const ray& r, const hittable& world) {
hit_record rec;
if (world.hit(r, 0, infinity, rec)) {
return 0.5 * (rec.normal + color(1, 1, 1));
}
vec3 unit_direction = unit_vector(r.direction());
auto t = 0.5 * (unit_direction.y() + 1.0);
return (1.0 - t) * color(1.0, 1.0, 1.0) + t * color(0.5, 0.7, 1.0);
}
int main() {
const auto aspect_raio = 16.0 / 9.0;
const int image_width = 384;
const int image_height = static_cast<int>(image_width / aspect_raio);
std::ofstream file("result.ppm");
file << "P3\n" << image_width << ' ' << image_height << "\n255\n";
auto viewport_height = 2.0;
auto viewport_width = aspect_raio * viewport_height;
auto focal_length = 1.0;
auto origin = point3(0, 0, 0);
auto horizontal = vec3(viewport_width, 0, 0);
auto vertical = vec3(0, viewport_height, 0);
auto lower_left_corner = origin - horizontal / 2 - vertical / 2 - vec3(0, 0, focal_length);
// シーンにオブジェクトを追加する.
hittable_list world;
world.add(make_shared<sphere>(point3(0, 0, -1), 0.5));
world.add(make_shared<sphere>(point3(0, -100.5, -1), 100));
for (int j = image_height - 1; j >= 0; --j) {
std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
for (int i = 0; i < image_width; ++i) {
auto u = double(i) / (image_width - 1);
auto v = double(j) / (image_height - 1);
auto direction = lower_left_corner + u * horizontal + v * vertical;
ray r(origin, direction);
color pixel_color = ray_color(r, world);
write_color(file, pixel_color);
}
}
std::cerr << "\nDone.\n";
return 0;
}これらを実行して結果を確認すると以下の画像が得られています。

アンチエイリアシング
実際のカメラで写真を撮る場合、エッジに沿ったギザギザは見えません。エッジピクセルは前景と背景のブレンドとなるためです。各ピクセル内の多数のサンプルを平均化することで、同じ効果を得ることが出来ます。

ここではカメラクラスを少し抽象化して作成し、後でクールなカメラを作成できるようにしておきましょう。
一部の乱数ユーティリティ
0≦R<1 の範囲内で正規乱数を返す乱数ジェネレーターが必要になります。最近の C++ では乱数ジェネレーターが使えるようになったので以下のようにしてここでは使っていきます。これも rtweekend.h に追記します。
#include <random>
inline double random_double() {
static std::uniform_real_distribution<double> distribution(0.0, 1.0);
static std::mt19937 generator;
return distribution(generator);
}複数のサンプルを持つピクセルの生成
1つのピクセル内に複数のサンプルがあるとして、ここからレイを送出します。このピクセルの色を決めるときには、レイが得た色を平均化して求めます。
カメラクラスを用意します。これは以前 main 関数の中で処理していたものを抽出したに過ぎません。
#include "rtweekend.h"
class camera {
public:
camera() {
auto aspect_ratio = 16.0 / 9.0;
auto viewport_height = 2.0;
auto viewport_width = aspect_ratio * viewport_height;
auto focal_length = 1.0;
origin = point3(0, 0, 0);
horizontal = vec3(viewport_width, 0.0, 0.0);
vertical = vec3(0.0, viewport_height, 0.0);
lower_left_corner = origin - horizontal/2 - vertical/2 - vec3(0, 0, focal_length);
}
ray get_ray(double u, double v) const {
return ray(origin, lower_left_corner + u*horizontal + v*vertical - origin);
}
private:
point3 origin;
point3 lower_left_corner;
vec3 horizontal;
vec3 vertical;
};マルチサンプルによるカラー計算をするために、 write_color 関数を修正します。色を求めるときには複数のサンプルリングで求められた色を加算し、最後で除算を行うようにします。
void write_color(std::ostream &out, color pixel_color, int samples_per_pixel) {
auto r = pixel_color.x();
auto g = pixel_color.y();
auto b = pixel_color.z();
// Divide the color total by the number of samples.
auto scale = 1.0 / samples_per_pixel;
r *= scale;
g *= scale;
b *= scale;
// Write the translated [0,255] value of each color component.
out << static_cast<int>(256 * clamp(r, 0.0, 0.999)) << ' '
<< static_cast<int>(256 * clamp(g, 0.0, 0.999)) << ' '
<< static_cast<int>(256 * clamp(b, 0.0, 0.999)) << '\n';
}main 関数についても修正します。本家ではサンプル数を1ピクセルあたり100サンプルとしており、かなり贅沢にレイを飛ばしていました。
int main() {
const auto aspect_raio = 16.0 / 9.0;
const int image_width = 384;
const int image_height = static_cast<int>(image_width / aspect_raio);
const int samples_per_pixel = 100;
std::ofstream file("result.ppm");
file << "P3\n" << image_width << ' ' << image_height << "\n255\n";
// シーンにオブジェクトを追加する.
hittable_list world;
world.add(make_shared<sphere>(point3(0, 0, -1), 0.5));
world.add(make_shared<sphere>(point3(0, -100.5, -1), 100));
camera cam;
for (int j = image_height - 1; j >= 0; --j) {
std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
for (int i = 0; i < image_width; ++i) {
color pixel_color(0, 0, 0);
for (int s = 0; s < samples_per_pixel; ++s) {
auto u = double(i+random_double()) / (image_width - 1);
auto v = double(j+random_double()) / (image_height - 1);
ray r = cam.get_ray(u, v);
pixel_color += ray_color(r, world);
}
write_color(file, pixel_color, samples_per_pixel);
}
}
std::cerr << "\nDone.\n";
return 0;
}この実行結果でピクセルエッジは滑らかになりました。一部分を拡大したものが以下です。

流石に100サンプルでは処理時間も今までよりも多くの時間が掛かることを体感できました。そこで、多くのグラフィックス系APIでよく見られる MSAA (Multisampling AntiAlias)での8倍の設定と同じくサンプル数 8 にしてみたもので画像を生成させてみました。一部分を拡大したものですが、やはり上記の100サンプルに比べるとエッジが汚いようです。

休憩
Ray Tracing in One Weekend を約半分まで追いかけてきました。今のところ形状が表示されているものの、法線情報でカラーリングしているのみです。今後はこれが各マテリアルを設定してレイトレーシングらしい画像に成長していくはずです。自分自身もこの先が楽しみです。
タイトルの通り、ここまでの内容で週末を消費しきることはないように思います。自分は始めた時間が悪かったこともあり、一旦ここで中断となってしまいましたが。ここまでの内容を連続時間でやるとしたら、2,3時間といったところでしょうか。
またこの続きも近いうちに更新出来ると思いますので、引き続きよろしくお願いします。

